Illustrations related to the many-sheeted space-time concept and the notions of TGD inspired theory of consciousness

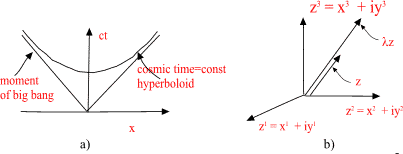
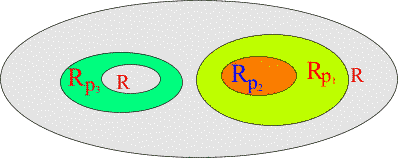
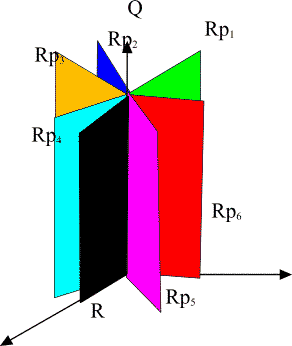
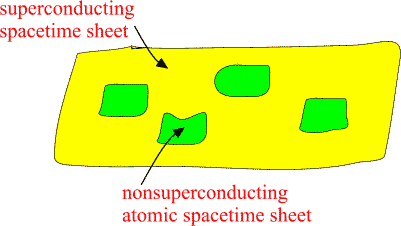
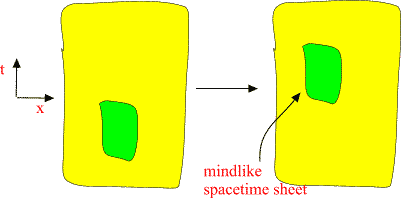
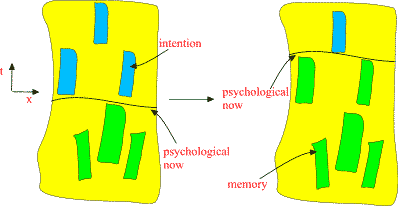
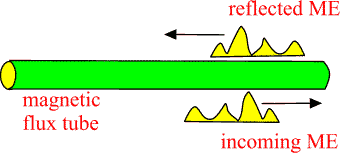
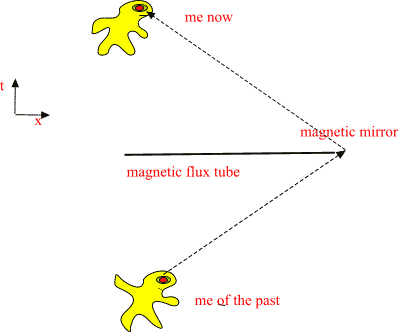
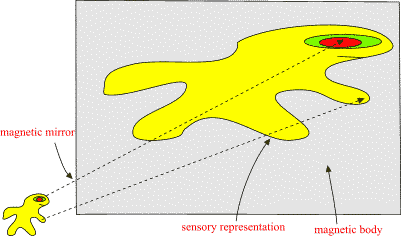
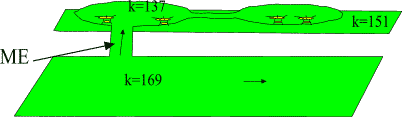
A. Visualizations of many-sheeted space-time concept

Figure 1: The presence of matter makes space-time curved and spoils translational and rotational symmetries: this means the loss of basic conservation laws.

Figure 2: a) Future lightcone M4₊ of Minkowski space. b) CP₂ is obtained from C³ by identifying the points related by complex scaling: z= lz .

Figure 3: An illustration of wormhole contacts between parallel space-time sheets having elementary particle size and of join along boundaries bonds which can have macroscopic length.

Figure 4: Two-dimensional illustration of the many-sheeted space-time. Space-time sheets are connected to each other by wormhole contacts.

Figure 5: Schematic representation of the decomposition of the space-time surface to p-adic and real regions.

Figure 6: Generalized imbedding space is union of all p-adic imbedding spaces H_p and real imbedding space H intersecting along rational points common to all (Q denotes rationals, R for reals, and R_p for p-adic numbers). In figure some of the immedding spaces H_p are illustrated as half-planes.

Figure 7: Atomic space-time sheets are at high temperature and non-superconducting as standard physics predicts but larger space-time sheets can have very low temperature and superconduct.

Figure 8: a) 2-dimensional space-time illustration of topological light ray (massless extremal, ME). Field pattern propagates with light velocity preserving its shape. b) MEs serve as field bridges between space-time sheets and make possible both classical and quantum communications.

Figure 9: The classical non-determinism of Kaehler action forces to generalize the notion of 3-surface by allowing sequences of space-like 3-surfaces with time-like separations. These sequences have interpretation as linguistic expressions providing a representation for quantum jump sequence defining the contents of consciousness of self.

B. Visualizations related to TGD inspired theory of consciousness

Figure 1: Schrödinger cat has no self identity because it entangles with a quantum bottle of poison and is simultaneously both dead and alive.

Figure 2: The simplest manner to understand psychological time is as the center of mass temporal coordinate for a mindlike space-time sheet. The arrow of psychological time results from the drift of the mindlike space-time sheet to the direction of future induced by the geometry of the future lightcone.

Figure 3: Psychological now corresponds to the phase transition front at which p-adic space-time regions (blue) representing intentions are transformed to real space-time regions representing actions and memories (green).

Figure 4: Fusion and sharing of mental images occurs if subselves (mental images) of two selves entangle to form a more complex 'stereo' mental image. This is not possible without length scale dependent notion of subsystem.

C. Visualizations related to the basic quantum mechanisms of consciousness and bio-control

Figure 1: The ends of the magnetic flux tube can act as mirrors at which topological light rays (MEs) are reflected. Oscillations of magnetic flux tube can also amplify the signals carried by MEs.

Figure 2: Mirror mechanism of long term memory. To remember is to look at magnetic mirror at distance of light years.

Figure 3: The transformation of intention to action corresponds to a quantum jump in which p-adic space-time region is transformed to a real one.

Figure 4: Magnetic mirrors (topological light rays associated with magnetic flux tubes) act as sensory projectors from brain (and body) to the magnetic body acting as sensory canvas.

Figure 5: MEs can serve as bridges between various space-time sheets. This induces a leakage of the supra currents from magnetic flux tubes (k=169) to the atomic space-time sheets (k=137) and vice versa. Also the time reversal of this process can occur (k=151 denotes cell membrane space-time sheet).

Figure 6: Many-sheeted space-time can be regarded as an extremely complex Feynman diagram with lines thickened to space-time sheets. The figure illustrates the idea for very simple Feynman diagram describing boson exchange.

To the beginning

To the index-page